A tree is a data structure with multiple branching, they are made up of nodes, and each tree has a root node, and each root node will have zero or more child nodes, and each child node in turn can also have zero or more child nodes etc. Nodes at the bottom of the tree, that is who have no children, are called leaf nodes. A tree can’t contain cycles, the nodes themselves can have any data type for their values, and these nodes may or may not link back to their parent nodes(Ref#: J).
The Tree data structure is considered a type of Graph.
Binary Trees
Binary trees as a data structure or type can be almost as fundamental as lists, and they can provide very efficient storage and retrieval of information. Binary Trees are known as a recursive data type, and functions on trees are expressed recursively using pattern-matching. Binary tree are trees where each node can only have up to 2 children (or 0-2 child nodes).
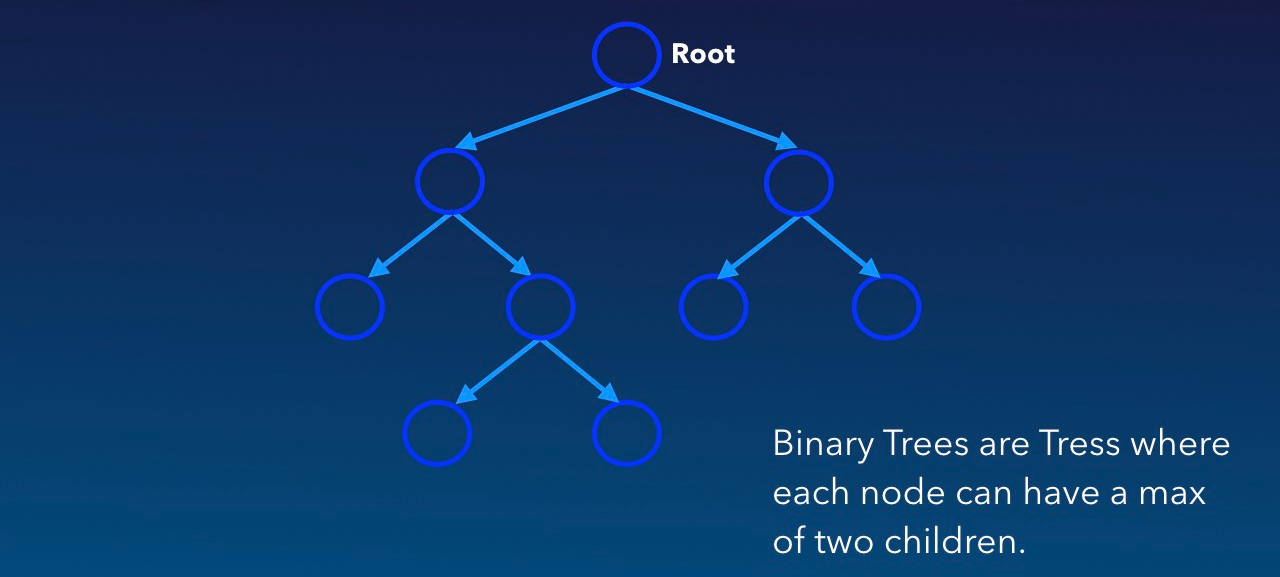
Binary Search Trees
One type of Binary Tree is a Binary Search Tree. This kind of tree has additional qualities compared with a simple Binary Search Tree:

In an interview context, if someone was to ask you about a Tree like this, it’s important to clarify whether the Tree they have asked you about is a Binary Search Tree, or just a Binary Tree, which doesn’t necessarily have the ordering properties of a BST. It is also important to clarify how a questioner is using the term BST and in particular if they are assuming a lack of duplicate values in the search tree.
Complete Binary Trees / Full Binary Trees / Perfect Binary Trees

Importance of Keeping BST Balanced
If your tree gets unbalanced, it can cause operation we perform on it to become inefficient, and equivalent to the complexity of a list for search, insert, and delete; we would prefer to avoid unbalanced BSTs.

Keeping a Balanced BST’s insures that max complexity of BST operation stays at O(log n):
|
Data Type by Big-O Operation Complexity |
||||
|
Unordered Array |
Linked List |
Sorted Array |
Balanced BST |
|
| Search(x) |
O(n) |
O(n) |
O(log n) |
O(log n) |
| Insert(x) |
O(1) |
O(1) |
O(n) |
O(log n) |
| Remove(x) |
O(n) |
O(n) |
O(n) |
O(log n) |
Implementation
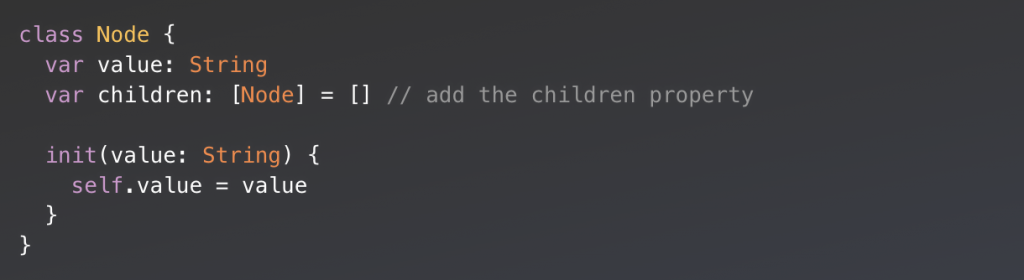
The simplest implementation of a Tree will start with a node class, if we start with the simplest node implementation which contain no reference to a parent node this might look like this:
So in Java:

And in Swift:
What we might then want to do is to create a Tree class which will have a root. If we want a binary tree, we might want a reference to the left and right child separately.
Here is a sample implementation of a simple binary tree class in Python:
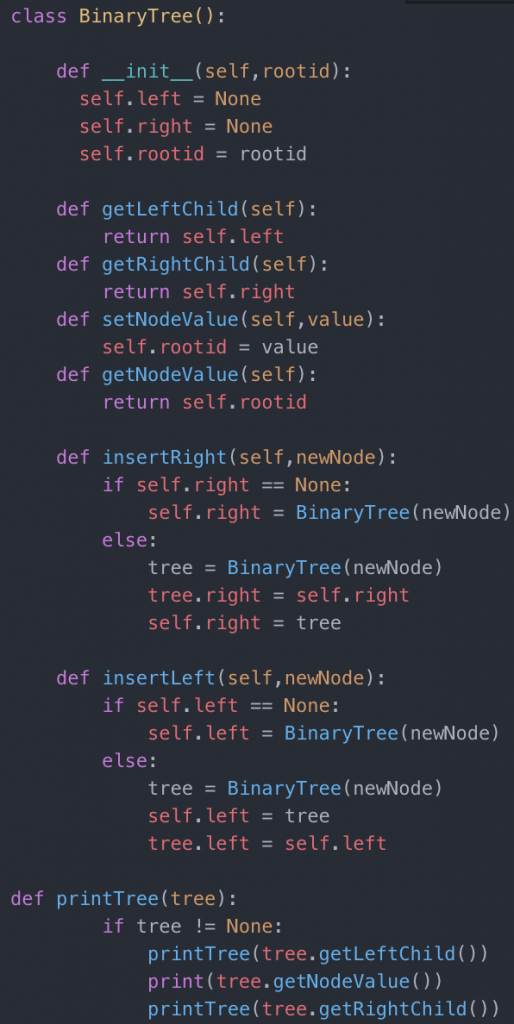
SOURCE: https://pythonschool.net/data-structures-algorithms/code/binary_tree.py
Binary Trees however are far from the only kinds of tree, as one may also have 10-ary tress which could have up to 10 children for example (which you might use for something like storing phone numbers).
Red-Black Tree
One method of keeping a binary tree balance is a Red-Black Tree: this is a type of self-balancing binary search tree where each node of the tree has an extra bit (red or black) where these color bits are used to ensure the tree remains fairly balanced during insertion and deletion operations.
- Each node in a red-black tree will be either red or black.
- The root and leaves of a red-black will always be black.
- For each red node, that nodes children will be black.
- All paths from a node to it’s nil descendants contain the same number of black nodes.
- Red-Black tress have a Maximum Height = O(log n)
In order for this type of tree to stick to the above rules defining its structure, RBT’s employ two techniques:
Recoloring and Rotation
Recoloring changes the color of a node based on some rules, either to red or black.
Whereas, rotation will change the structure of a given tree by re-arranging subtrees with the goal of decreasing the height of the tree.
Where we see this happening is in the rules governing insertion and deletion:
https://www.geeksforgeeks.org/red-black-tree-set-2-insert/
AVL Trees
Comparisons with Red-Black Trees
“The AVL trees are more balanced compared to Red-Black Trees, but they may cause more rotations during insertion and deletion. So if your application involves many frequent insertions and deletions, then Red Black trees should be preferred. And if the insertions and deletions are less frequent and search is a more frequent operation, then AVL tree should be preferred over Red-Black Tree”()
Traversing a Tree
We may traverse our tree either using a Depth-First approach or alternatively using a Breadth-First (or level-order) approach. In a depth-first approach we go down to the right to the leaf nodes of our first subtree from our root, before then moving on to the second subtree descending form the root etc. Algorithms based on these notions typically perform some action at each node.
With a Breadth-First approach, we start at the top of the tree and we traverse level by level, that is to say we go through all the nodes that are one level down in a tree no matter what sub-tree they are a part off, then the same for two levels down etc.
Within the Depth-First approach there is: In-Order Traversal, Pre-Order Traversal, and Postorder Traversal.
- In-Order Traversal goes in the order of : <left>, <root>, <right>.
- A Pre-Order Traversal traverses in the order: <root>, <left>, <right>.
- Finally Post-Order Traversal is done in the order of: <left>, <right>, <root>.
Tries
When we talk about Trees we need to also mention the so-called “Trie” data-structure. “A trie, also called digital tree and sometimes radix tree or prefix tree (as they can be searched by prefixes), is a kind of search tree that is used to store a dynamic set or associative array where the keys are usually strings. Unlike a binary search tree, no node in the tree stores the key associated with that node; instead, its position in the tree defines the key with which it is associated“ (Source: wikipedia).

Conclusion
In this post we reviewed what Trees are and how they can be useful. Specifically we looked at the tree data-structure. Furthermore, we also covered the two well known ways of keeping our tree balanced, namely the Red-Black Tree, or the AVL Tree.
References
A: http://www.cl.cam.ac.uk/teaching/exams/pastpapers/y2017p1q7.pdf
B: https://www.youtube.com/watch?v=oSWTXtMglKE
C: http://software.ucv.ro/~mburicea/lab8ASD.pdf
D: https://www.youtube.com/watch?v=9RHO6jU–GU
E: https://en.wikipedia.org/wiki/Trie
F: https://www.geeksforgeeks.org/binary-search-tree-set-1-search-and-insertion/
G: https://www.geeksforgeeks.org/red-black-tree-set-2-insert/
H: http://www.cl.cam.ac.uk/teaching/1617/FoundsCS/fcs-notes.pdf
I: https://ocw.mit.edu/courses/electrical-engineering-and-computer-science/6-046j-introduction-to-algorithms-sma-5503-fall-2005/video-lectures/lecture-10-red-black-trees-rotations-insertions-deletions/
J: McDowell, G. L. (2016). Cracking the Coding Interview: 6th Edition. Career Cup, Palo Alto, CA.
K: https://www.raywenderlich.com/1053-swift-algorithm-club-swift-tree-data-structure
![]()
Comments